How Does Logistic Regression Work? Everything You Need to Know
Logistic regression is a technique used to predict the probability of an event occurring by classifying data into categories.
First of all, I wish you a Happy 2025! ✨
May this new year be full of achievements, learning, and new opportunities. And to start off on the right foot, let’s explore a very interesting concept: logistic regression!
Logistic regression is a widely used technique in data analysis and machine learning, especially in classification tasks.
Unlike linear regression, which is used to predict continuous variables, logistic regression is used to predict categorical variables, typically with two classes (binary) – for example, the probability of a customer buying or not buying a product.
Let’s understand how this technique works, and at the end of the article, we’ll get hands-on with a practical example!
You can find the code on Colab at: https://exploringartificialintelligence.substack.com/p/notebooks
What is Logistic Regression?
The goal of logistic regression is to model the probability of a binary dependent variable (0 or 1) based on one or more independent variables.
The main idea behind the model is to use a sigmoid function (also known as the logistic function) to transform the linear prediction into a probability.
The sigmoid function is a mathematical curve that transforms values into a range between 0 and 1, commonly used in machine learning models to represent probabilities.
The equation for logistic regression is expressed as:
Where:
P(Y=1|X) is the probability that the dependent variable Y equals 1, given the independent variable X.
β₀ is the intercept (or bias coefficient).
β₁ is the coefficient of the independent variable X.
e is the base of the natural logarithm, approximately 2.718.
The sigmoid function maps the values of the linear equation to the range of 0 to 1, interpreting these values as probabilities.
How It Works
The training process of a logistic regression model involves estimating the coefficients (β₀, β₁, etc.) in such a way that the model minimizes the error between the predictions and the actual values.
The most common technique for optimizing these coefficients is the maximum likelihood method, which seeks to find the values that make the data most probable, given the distribution of the residuals.
Application Examples
Medical Diagnosis: Predict whether a patient has a disease based on characteristics such as age, medical history, and test results.
Credit Analysis: Evaluate whether a customer should be approved for credit based on variables like income, credit history, and other financial data.
Marketing and Sales: Predict the probability of a customer making a purchase based on their browsing behavior or demographic characteristics.
Advantages of Logistic Regression
Simple and Efficient: It's easy to understand and interpret, with a simple mathematical formulation.
Probability as Output: Logistic regression provides an interpretable output as a probability, which is useful in many decision-making situations.
Works Well with Linear Data: If the relationship between the independent variables and the dependent variable is linear, logistic regression is quite effective.
Limitations
Restricted to Binary Variables: Although there are variations (like multinomial logistic regression), basic logistic regression is suitable only for binary classification tasks.
Sensitive to Outliers: The presence of outliers (values that deviate significantly from the data pattern) can significantly influence the estimation of coefficients.
Linear Relationships: It assumes that the relationship between the independent variables and the dependent variable is linear on the log odds of the probabilities, which may not be the case in some more complex situations.
Difference Between Linear Regression and Logistic Regression
The main difference between linear regression (which we saw earlier) and logistic regression lies in the type of dependent variable each one handles.
Linear regression is used to predict continuous variables, such as price or temperature, and models the relationship between independent and dependent variables with a straight line.
Logistic regression is used when the dependent variable is binary or categorical, like "yes" or "no," and makes probability predictions by applying the sigmoid function to ensure that the outputs fall between 0 and 1.
While linear regression generates continuous values without restrictions, logistic regression transforms its predictions into probabilities, ideal for classification tasks.
Let's code!
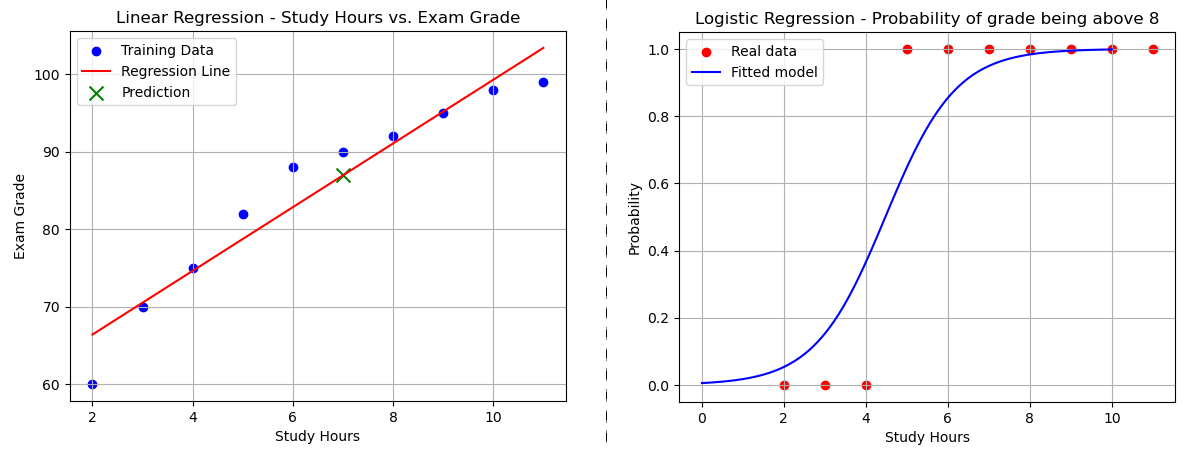
We will continue with the example from our article on linear regression, which involves the number of hours studied and students' grades.
However, instead of predicting the grade directly, as we did with linear regression, we will now use Logistic Regression to predict the probability of a student scoring above 8.
Here’s the Python code:
import numpy as np
from sklearn.linear_model import LogisticRegression
import matplotlib.pyplot as plt
# Data provided in the problem
study_hours = np.array([2, 3, 4, 5, 6, 7, 8, 9, 10, 11]).reshape(-1, 1)
grades_above_8 = np.array([0, 0, 0, 1, 1, 1, 1, 1, 1, 1])
# Create and train the logistic regression model
model = LogisticRegression()
model.fit(study_hours, grades_above_8)
# Make predictions and calculate the probability for values in the range
x_values = np.linspace(0, 10, 100).reshape(-1, 1)
y_prob = model.predict_proba(x_values)[:, 1]
# Visualize the results
plt.scatter(study_hours, grades_above_8, color="red", label="Real data")
plt.plot(x_values, y_prob, color="blue", label="Fitted model")
plt.xlabel("Study Hours")
plt.ylabel("Probability")
plt.title("Logistic Regression - Probability of grade being above 8")
plt.legend()
plt.grid()
plt.show()Result:
You can find the code on Colab at: https://exploringartificialintelligence.substack.com/p/notebooks
Conclusion
Logistic regression is a fundamental technique in the fields of statistics and machine learning, widely used across various domains.
Its ability to model probabilities and provide interpretable results makes it a powerful tool for solving classification problems.
By understanding the concepts behind logistic regression, you'll be well-equipped to apply it in a variety of data analysis scenarios.
In the next post, we’ll explore decision trees.
Stay tuned! 💗